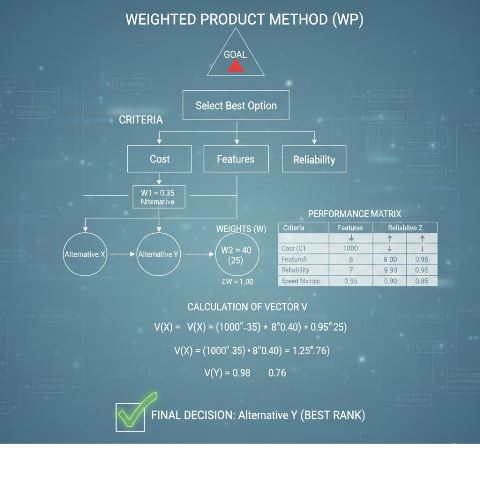
Unikma.ac.id – Metode WP adalah salah satu teknik dalam Pengambilan Keputusan Multikriteria (MCDM) yang digunakan untuk mengevaluasi dan merangking sejumlah alternatif berdasarkan kriteria-kriteria yang telah ditentukan. Metode ini dikembangkan oleh Miller dan Starr pada tahun 1969.
Metode Weighted Product (WP)
Metode Weighted Product (WP) menggunakan teknik perkalian untuk menghubungkan nilai atribut, di mana bobot (weight) digunakan sebagai pangkat (exponent) dari nilai kriteria. Konsep utamanya adalah mencari alternatif terbaik dengan membandingkan nilai total dari hasil perkalian kriteria (preferensi relatif) yang telah dipangkatkan dengan bobot kriteria.
Tahapan Dasar WP
Penerapan metode WP dalam SPK melibatkan langkah-langkah sistematis sebagai berikut:
- Normalisasi Bobot Kriteria ($W_j$)
Bobot kriteria harus dinormalisasi agar total seluruh bobot adalah 1 ($\sum W_j = 1$). Normalisasi dilakukan dengan membagi bobot setiap kriteria ($w_j$) dengan total bobot seluruh kriteria ($\sum_{j=1}^n w_j$).
$$W_j = \frac{w_j}{\sum_{j=1}^n w_j}$$
- $W_j$: Bobot ternormalisasi untuk kriteria ke-$j$.
- $w_j$: Bobot kriteria awal untuk kriteria ke-$j$.
Catatan: Dalam metode WP, kriteria dibagi menjadi dua jenis: Kriteria Keuntungan (Benefit) dan Kriteria Biaya (Cost).
- Menentukan Bobot Pangkat Kriteria
Untuk kriteria keuntungan (benefit), nilai bobot ternormalisasi ($W_j$) tetap positif.
Untuk kriteria biaya (cost), nilai bobot ternormalisasi ($W_j$) dijadikan negatif (sebagai pembalik), karena nilai yang lebih kecil (cost rendah) lebih disukai.
$$P_j = \begin{cases} W_j & \text{jika } j \text{ adalah kriteria benefit} \\ -W_j & \text{jika } j \text{ adalah kriteria cost} \end{cases}$$
- Menghitung Nilai Vektor $S_i$ (Preferensi Relatif)
Nilai Vektor $S_i$ untuk setiap alternatif ($i$) diperoleh dengan mengalikan nilai kriteria ($x_{ij}$) yang telah dipangkatkan dengan bobot pangkat ($P_j$) yang sudah disesuaikan.
$$S_i = \prod_{j=1}^n (x_{ij})^{P_j}$$
- $S_i$: Nilai preferensi relatif untuk alternatif ke-$i$.
- $x_{ij}$: Nilai rating alternatif ke-$i$ pada kriteria ke-$j$.
- $P_j$: Bobot pangkat kriteria ke-$j$.
- Menghitung Nilai Vektor $V_i$ (Prioritas Relatif)
Nilai Vektor $V_i$ adalah nilai total preferensi yang digunakan untuk perankingan. Nilai ini diperoleh dengan membagi nilai $S_i$ dari setiap alternatif dengan total seluruh nilai $S$ dari semua alternatif.
$$V_i = \frac{S_i}{\sum_{i=1}^m S_i}$$
- $V_i$: Nilai prioritas relatif (Vektor $V$) untuk alternatif ke-$i$.
- $\sum_{i=1}^m S_i$: Jumlah total nilai $S$ dari semua alternatif ($m$).
- Perangkingan
Alternatif yang memiliki nilai $V_i$ tertinggi adalah alternatif yang paling direkomendasikan atau memiliki preferensi tertinggi dalam sistem penunjang keputusan.
—
Penulis: Slamet Edy Cahyo, M.Kom, dosen Universitas Komputama (UNIKMA), Cilacap, Jawa Tengah
Editor: Muhamad Ridlo
Referensi
Berikut adalah beberapa jenis referensi penting untuk memahami dan mengimplementasikan metode Weighted Product (WP):
- Miller, D. W., & Starr, M. K. (1969). Executive Decisions and Operations Research. Prentice-Hall, New York.
- Kusrini (2007, atau edisi terbaru). Konsep dan Aplikasi Sistem Pendukung Keputusan. Penerbit Andi, Yogyakarta.
- Fishburn, Peter C.(1970). Utility Theory for Decision Making. John Wiley & Sons.
- Nofriansyah, D., & Defit, S. (2017). Multi Criteria Decision Making Pada Sistem Penunjang Keputusan. Deepublish.